The goal of this univeristy project was to implement a simulation of cloth model as a skirt on a dancer. The simulation is implemented in Unreal Engine 5.0.3.
The project was done in pairs, however, I am presenting here the whole result, we were working on it equally without any specific division.

Cloth simulation is an inseparable part of modern computer graphics, including the entertainment industry aiming for realistic depiction. However, the problem with the simulation is the realistic approach, as the cloth behavior is challenging to simulate.
This work focuses on the implementation of the skirt on a dancer using the presented mass-spring model in Unreal Engine.
The first section presents the description of the discrete mesh representation with the mass-spring cloth model; it follows the details of the implementation where the algorithm is described in detail and results with provided images of the final result.
Cloth models
Discrete Mesh Representation—Mass-Spring Model: Provot in his work [1] came up with the idea of representing the cloth as a discrete mesh representation with mass-spring forces. In this representation, the mesh structure represents the cloth by a set of massfull particles on a grid. These particles are connected to each other by massless springs to simulate the behavior of the cloth. The springs are of three types based on what they are responsible for on the cloth. These springs are responsible for the stretch, shear, or bend forces acting on the particles. The springs and their position based on the spring type are visualized in Figure 1.
These rules set the position of the specific type of spring: • Structural springs connect particles with indexes [i,j] and [i+1, j], and [i,j] and [i, j+1] • Shear springs connect particles with indexes [i,j] and [i+1, j+1], and [i+1,j] and [i, j+1] • Flexion springs connect particles with indexes [i,j] and [i+2, j], and [i,j] and [i, j+2]
![Types of spring: a) Structural springs, b) Shear springs, c) Flexion springs [2]](/images/pages/MMA/SpringForces.png)
Types of spring: a) Structural springs, b) Shear springs, c) Flexion springs [2]
Forces
The principle of the dynamics of the simulation is based on Newton’s law:
\[F = ma\]where:
- m is the mass, and
- a is the acceleration of the particle.
The mesh is represented by $h \times w$ masses stored in a grid, and for each particle in the system, a force $F$ acting on it is calculated.
The force is calculated from the internal spring forces and external forces like gravity, wind, etc. Each particle is positioned at time $t$ at the point $P_{i,j}(t)$, where $i = 1, \ldots, w$ and $j = 1, \ldots, h$.
Dynamics of the System
The dynamics of the system are computed as follows:
\[F_{i,j} = \mu a_{i,j}^2\]where: μ is the mass of each point (Pi,j), and (ai,j) is its acceleration [3].
The position $P_{i,j}(t + 1)$ for mass $(i, j)$ is calculated as:
\[a_{i,j}(t + \Delta t) = \frac{1}{m} F_{i,j}(t)\] \[v_{i,j}(t + \Delta t) = v_{i,j}(t) + \Delta t \cdot a_{i,j}(t + \Delta t)\] \[P_{i,j}(t + \Delta t) = P_{i,j}(t) + \Delta t \cdot v_{i,j}(t + \Delta t)\]Internal Spring Force
The internal spring force $F_s$ is calculated according to Hooke’s law:
\[F_{s, i,j} = -k_s \left( \lvert x_i - x_j \rvert - r \right) \frac{x_i - x_j}{\lvert x_i - x_j \rvert}\]where:
- $x_i - x_j$ is the difference between the positions of the two particles,
- $r$ is the rest length of the spring, and
- $k_s$ is the elastic modulus of the spring.
The value of $k_s$ should be:
- Large for structural springs, and
- Small for shear and flexion springs [3].
Damping Forces
Damping forces represent energy dissipation due to internal friction. These forces are modeled as:
\[F_{d, i,j} = d \frac{(v_i - v_j)(x_i - x_j)}{\lvert x_i - x_j \rvert^2}(x_i - x_j)\]where:
- $d$ is the damping factor.
Addressing “Super-Elastic” Effects
Provot [1] observed that cloth could behave unrealistically when it is hanging with some fixed points. He noted that cloth should elongate only by a maximum of 10%, but this is not achieved when springs are elongated by more than 100% of their natural length.
Proposed Solution
Provot proposed a solution by thresholding the deformation rate in structural and shear springs. The deformation occurs mostly at points connected to fixed corners.
To avoid the so-called “super-elastic” effect:
- Increase the damping coefficient.
- Implement an ad hoc dynamic inverse procedure for affected springs to lower their elongation.
Critical Deformation Rate
If the deformation rate of a spring exceeds a critical deformation rate $\tau_c$, then the inverse procedure is applied. For example:
- If $\tau_c = 0.1$, springs are not prolonged by more than 10% of their natural length.
The distance reduction is done differently based on the node configurations:
-
Both nodes are loose:
Both nodes are evenly brought together to the middle of the spring until the shrinking rate reaches $\tau_c$. -
Only one node is loose:
The loose node is brought closer to the fixed node until the shrinking rate reaches $\tau_c$. -
Both nodes are fixed:
These nodes remain unchanged.
Implementation
The animation was presented in Unreal Engine 5.0.3 [6] with the code written in C++ and the blueprint.
The algorithm 1 illustrates the creation of springs connecting the nodes.
Algorithm 1: Spring Creation
Procedure 1: PROCESSNODES(allNodes)
- For each 6 nodes:
AddSpringsToNodes(ni, ..., ni+5)
- For each node
ni:- Connect node
niand its right neighbor with a structural spring - Connect node
niand its up neighbor with a structural spring - Connect node
niand the right neighbor of its right neighbor with a flexion spring - Connect node
niand the up neighbor of its up neighbor with a flexion spring
- Connect node
Procedure 2: ADDSPRINGSTONODES(n1, n2, n3, n4, n5, n6)
- Let
a1, a2, a3be nodes from the first triangle - Let
b1, b2, b3be nodes from the second triangle - Add neighbors to nodes
a1, a2, a3based on their relative positions - Add neighbors to nodes
b1, b2, b3 - Compare nodes
a1-3with nodesb1-3and determine the shared nodes - From the triangle vertices, remove the shared vertices and find unique vertices in each triangle
- Connect
sharedNode1andsharedNode2with a shear spring - Connect
uniqueNode1anduniqueNode2with a shear spring
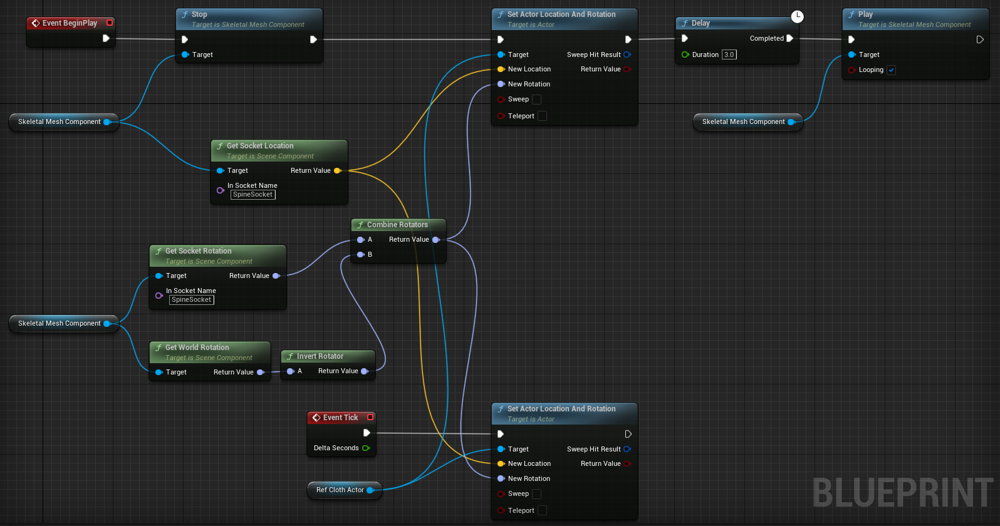 Blueprint for the human character
Blueprint for the human character
Implementation difficulties
One of the difficulties we encountered during the implementation was converting the skirt mesh asset created from the fbx file to the grid and the mesh. Since Unreal Engine cannot deal with sharp edges, it duplicates vertices resulting in the dynamic mesh not being continuous. It was necessary to create a map of each created Node of the grid and its position not to have duplicate Nodes in the final mesh.
The vertices are also not stored in any particular order so just using the indexing provided in the section 2 to connect particles with a correct spring was not possible. Unreal Engine always stores a pair of triangles together that share one diagonal edge in the mesh. This helped with the decision of which nodes need to be connected by the structural spring and which nodes need to be connected by the shear spring.
The flexion springs were however more difficult to add. For each node, it was necessary to store its neighbors based on the position of the neighbor relative to the node. This means storing its right neighbor and the neighbor sitting directly below on the grid.
Relocation fixed nodes to the spine’s location brings us a quagmire. Rotation of the spine bone has different local coordinates from the skirt model and the character model whose have a world coordinates thus the blueprint became more complicated.
One of the mysteries of our project is a crashing of the simulation when we input 3D model with more vertices. In our opinion it can be caused by calling an unstable function AddForce which could be dependent on the number of FPS.
Results
The final simulation was tested on the university’s computer which has following parameters: Intel(R) Core(TM) i9-10900x CPU @ 3.70GHz, 10 Core(s);RAM 32 GB; GPU NVIDIA GeForce GTX 1070 Ti. The simulation was running with thoroughly chosen parameters which can be seen below.
The resulting images 3 show us the simulated skirt on which we can recognise some parts where the skirt is hidden under the human body. Due to the required computer performance, we had to use the simplest 3D model of the skirts. That can be one of the factors why the skirt overlaps with the human character. In Figure 4 we can see how simple the model is. This image presents structure of the cloth springs between mesh’s vertices.
 |
 |
|---|---|
| Representation of the particles in animation | Illustration of the collision objects |
References
[1] Xavier Provot. Deformation constraints in a mass-spring model to describe rigid cloth behavior. In Wayne A. Davis and Przemyslaw Prusinkiewicz, editors, Graphics Interface ’95, pages 147–154. Canadian Human-Computer Communications Society, 1995.
[2] Shin-Wen Hsiao, Rong-Qi Chen. A Method of Drawing Cloth Patterns With Fabric Behavior. Department of Industrial Design, National Cheng Kung University, 2006.
[3] Provot, Xavier. (2001). Deformation Constraints in a Mass-Spring Model to Describe Rigid Cloth Behavior. Graphics Interface. 23(19).
[6] Epic Games, 2019. Unreal Engine, Available at: https://www.unrealengine.com.
Comments